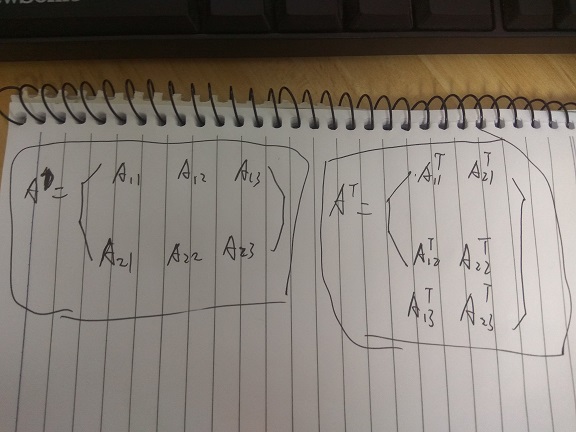
如图，左边的是分块矩阵（转置前），右边是分块矩阵转置后。之所以可以这样写，是因为矩阵关于的行数和列数中最大值的对角线进行互换元素。因此对于子矩阵这些个体来说，他们就可以写成右边的形式，但至于右边的形式展开后是否真的就等于左边的转置。其实理解起来也很简单。

首先，对于每个子矩阵来说，他们的转置方式（或性质）都和母矩阵A一样。即，没有一个子矩阵均是关于同一个平行的对角线互换元素。如果把母矩阵中的每个元素抽象成点，由此最外围的点构成的四边形进行折叠，即可得出形为A转置后将元素抽象成点的图像。证明下图中右边的式子就是A的转置。